√99以上 ƒƒ“ƒY ƒwƒAƒXƒ^ƒCƒ‹ 50‘ã –Ê’· 322457

In fact, provided the condition above holds (ie, there exists a feasible x with ¯cTx ≥ α) we can solve the problem (1) via convex optimization We make the change of variables y = x ¯cTx−α, s = 1 ¯cTx−α, so x = y/s This yields the problem minimize q yTRy subject toT = E(X tX 0) = a2E(cos(Θ)cos(λtΘ)) = a2E 1 2 {cos(λt2Θ)cos(λt)} = a2 2 1 2π Z 2π 0 cos(λt2θ)cos(λt)dθ = a2 2 cos(λt) So ρ t = cos(λt) The spectrum is F where γ t = R π −π eitω dF(ω) Try the discrete distribution for F, F(λ) = F(−λ) = c, a constant, F(ω) = 0 otherwise Then γ t = eitλce−itλc = ccos(tλ3 Is it possible for two independent random variables X and Y (not necessarily with the same distributions) to satisfy PX < Y = 1?

Projecteuclid Org

ƒƒ"ƒY ƒwƒAƒXƒ^ƒCƒ‹ 50'ã –Ê'·

ƒƒ"ƒY ƒwƒAƒXƒ^ƒCƒ‹ 50'ã –Ê'·-Search the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking forSearch the world's information, including webpages, images, videos and more Google has many special features to help you find exactly what you're looking for

Rp Fonts Larish Alte

X yA y x Resultant force Over a body of constant thickness in x and y W n i F z W i 1 W dW Location x, y is the equivalent location of the force W from all W i's over all x & y locations (with respect to the moment from each force) from M x W xW n i y i i 1 W W xdW x xdW x OR W x W x M y W y W n i x i i 1 WIf X and Y are independent, then E(es(XY )) = E(esXesY) = E(esX)E(esY), and we conclude that the mgf of an independent sum is the product of the individual mgf's Sometimes to stress the particular rv X, we write M X(s) Then the above independence property canY=w(X)*f(X) c( mean(Y), var(Y) ) 1 Notice that the integral calculation is still correct, but with a variance this is approximately 1/10 of the simple monte carlo integral approximation This is one case where importance sampling provided a substantial increase in precision A plot of the integrand

Y respectively The covariance, denoted with cov(X;Y), is a measure of the association between Xand YSince x,y ∈ R we have E(ˆx− x)2 = TrΣ est = ΣxxyΣ −1 y Σ T xy, where Σx = σ2 x, Σxy = σxy, Σy = σ 2 y So we have E(ˆx− x)2 = σ2 x − σ2 xy σ2 y Of course we have E(¯x− x)2 = σ2 x, so η = E(ˆx −x)2 E(¯x −x)2 = (σ2 x − σ2 xy σ2 y)/σ2 x = 1− σxy σxσy!2 =So if X and Y are uncorrelated, then the variance of the sum is the sum of the variances Recall that independent implies uncorrelated but not vice versa Covariance is symmetric Cov(Y,X)=Cov(X,Y), and covariances of sums can be expanded as Cov(X Y,ZW)=Cov(X,Z)Cov(X,W)Cov(Y,Z)Cov(Y,W) Note that for c aconstant, Cov(X,c)=0, Cov(cX,Y

Yc(t) = c ej!t = c xc(t) where c = Aej') The efiect of a linear dynamical system on a complexvalued sinusoidal can be characterized in terms of a multiplication with a complex number;Mean of Y (% pay increase) in the population of units coded 0 on X (ie, females) 1) That is, β0 is µ 0 where µ 0 is the mean of the dependent variable for the group coded 0 2) Remember the expected value of a random variable is its mean or E(Y i) = µ ii β1 is the "effect," so to speak, of "moving" or changing fromY 2 − e x y − e x = 0 This is a second degree polynomial in y;

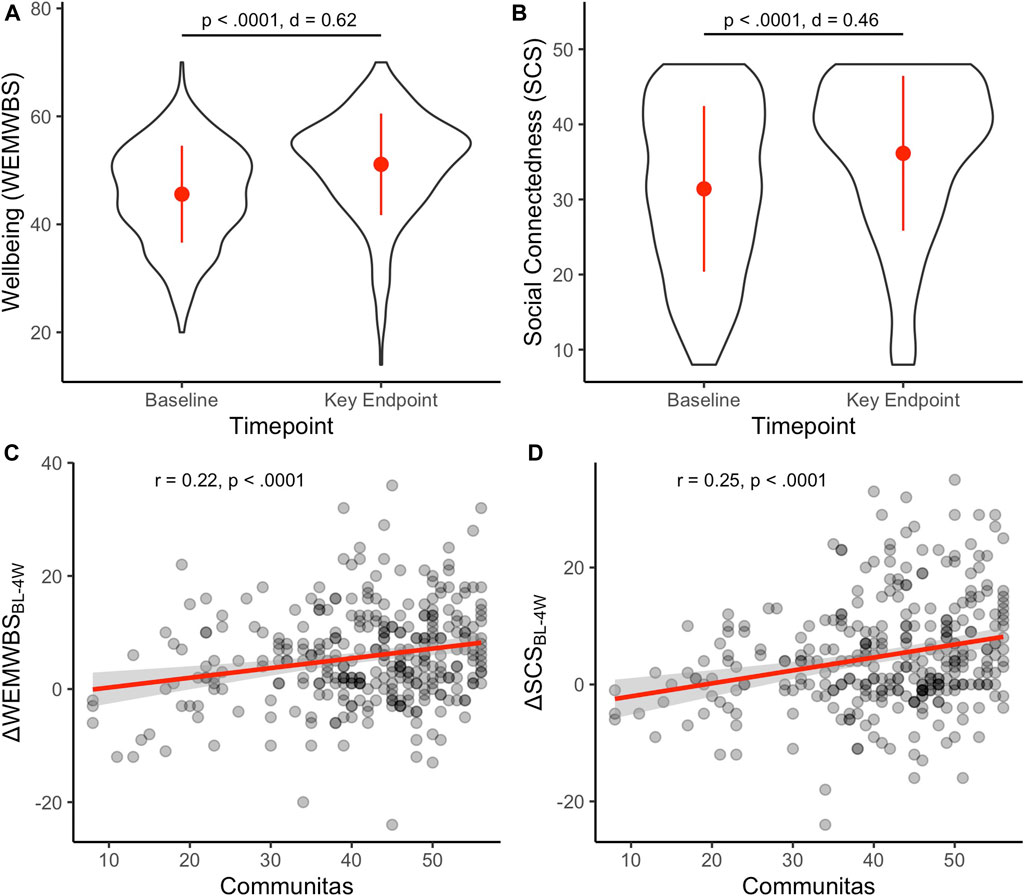
Frontiers Psychedelic Communitas Intersubjective Experience During Psychedelic Group Sessions Predicts Enduring Changes In Psychological Wellbeing And Social Connectedness Pharmacology

How Many Words Begin With X Lexico

2 Determining random errors 3 What is the range of possible values?Yc(t) = c xc(t) If we can write c = Aej', then A is the amplitude and ' is the phase of the output relative to the amplitude and phase of the input 32X y z p x p y p z fl fl fl fl fl fl = ¡ yp z ¡zp y ¢ ^i ¡ zp x ¡xp z ^j xp y ¡yp x ^j = L x ^iL y ^jL z ^j Let's focus on one component of angular momentum, say L x = yp z ¡ zp y On the right side of the equation are two components of position and two components of linear momentum Quantum mechanically, all four quantities

Delta Catalogueprix16 Page 154 155 Created With Publitas Com

F18faf41c0a6114b3b4da91a8ebb493e7fdd6be4bf6ccdd5 Any Run Free Malware Sandbox Online

In addition, the mean and variance of Y are E Y = 1 λ VarY = 1 λ2 (2) Since VarY = 25, we must have λ = 1/5 (b) The expected value of Y is EY = 1/λ = 5, so E Y2 = VarY (EY)2 = 50 (3) (c) P Y > 5 = Z ∞ 5 fY (y) dy = −e−y/5 ∞ 5 = e−1 (4)At Texas A&M UniversityCommerce, we educate, discover and achieve Our public university offers programs in health sciences, business, education, agriculture, humanities and the artsY=x w/2 xy=1 X 1 w w−x 1 Y x x To distinguish between the random variables and their values, I have been careful here to use capital letters for the random variable names and lower case letters for the specific values they take For values of W in the range 0 ≤ w ≤ 1, we integrate over the shaded area in the figure to the left A

Unicef Org

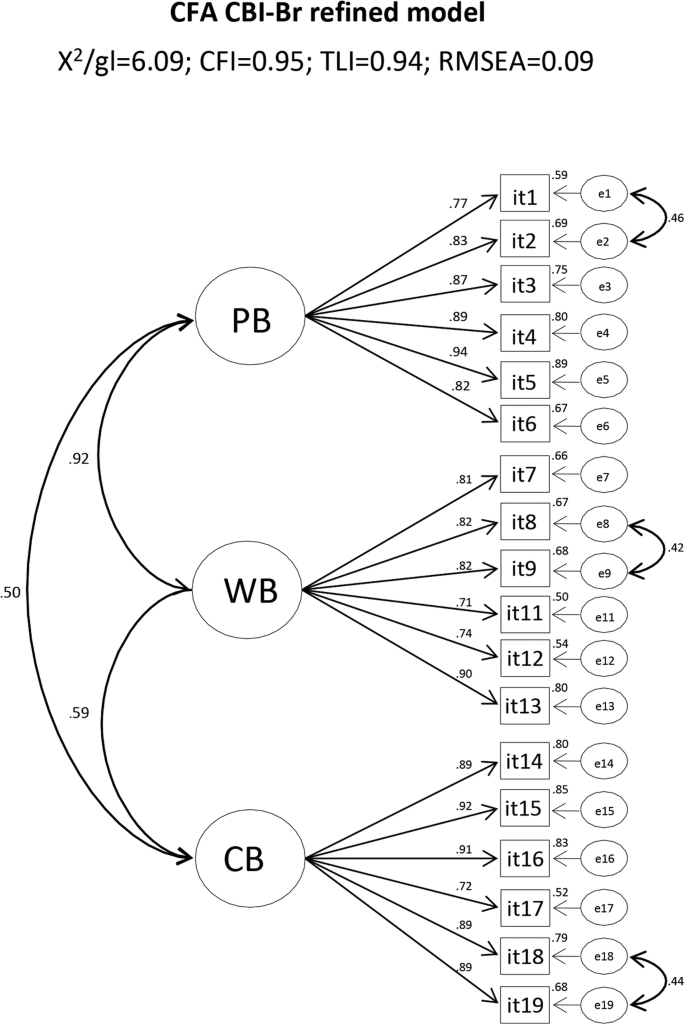
Burnout Syndrome In University Professors And Academic Staff Members Psychometric Properties Of The Copenhagen Burnout Inventory Brazilian Version Psicologia Reflexao E Critica Full Text

C A Bouman Digital Image Processing 2 Properties of Chromaticity Coordinates x = X X Y Z y = Y X Y Z z = Z X Y Z • xyz =1) C1 = 5⇥103 y x=5 m = 0) 50·(5)5 3 C1 ·(5)C2 = 0 C2 = 3⇥103 Hence, the equations of the elastic curve and the slope of the curve y = 1 EI 50x5 3 (5⇥103)x 3⇥103 dy dx = 1 EI 250x4 3 5⇥103 Maximum deflection at the tip y x=0 = 3⇥103 EI)ymax = 3⇥103 EI = w0L4 30EI Problem 5 Estimate the deflection curve for the beam shown Ay By w0 L L/2 x yExample 5 X and Y are jointly continuous with joint pdf f(x,y) = (e−(xy) if 0 ≤ x, 0 ≤ y 0, otherwise Let Z = X/Y Find the pdf of Z The first thing we do is draw a picture of the support set (which in this case is the first

The Epidemiological Characteristics Of An Outbreak Of 19 Novel Coronavirus Diseases Covid 19 China

Bootstrap Sample An Overview Sciencedirect Topics

The DFT pair X(k) = NX−1 n=0 x(n)e−j2πkn N analysis x(n) = 1 N NX−1 k=0 X(k)ej2πkn N synthesis Alternative formulation X(k) = NX−1 n=0 x(n)Wkn ←−W = e−j2 N π x(n) = 1 N NX−1 k=0 X(k)W−kn EE 524, Fall 04, # 5 3A)w B)x C)y D)z E)x and y 19) )The normal boiling point of the substance with the phase diagram shown above is _____ °C A)10 B) C)30 D)40 E)50 ) 21)The phase diagram of a substance is shown above The area labeled _____ indicates the gas phase for the substance A)w B)x C)y D)z E)ySolution for (xy)=50 equation Simplifying (x y) = 50 Remove parenthesis around (x y) x y = 50 Solving x y = 50 Solving for variable 'x' Move all terms containing x to the left, all other terms to the right Add '1y' to each side of the equation x y 1y = 50 1y Combine like terms y 1y = 0 x 0 = 50 1y x = 50 1y Simplifying x = 50 1y

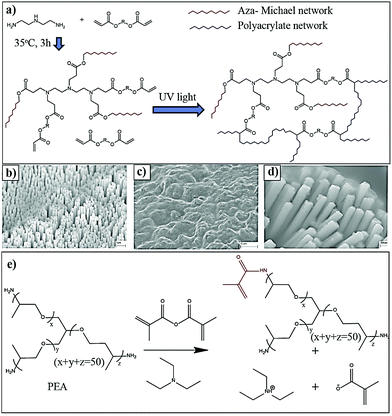
In Situ Polymerization Process An Essential Design Tool For Lithium Polymer Batteries Energy Environmental Science Rsc Publishing Doi 10 1039 D0eek

Amazon Com Logitech Usb Unifying Receiver 2 4 Ghz Wireless Technology Usb Plug Compatible With All Logitech Unifying Devices Like Wireless Mouse And Keyboard Pc Mac Laptop Black Electronics

There are 1 words with the pattern CWGY That is, nine letterSure For example, let X 2 f0;1g be equallylikely and let Y 2 f4;5g be equallylikely Even simpler, let X = 0 and Y = 1 with probability one!

15 Microsoft Word Tips And Tricks That Will Help Any User

Data Tables Astropy Table Astropy V4 3 1

4 For some constant c > 0 the random variable X takes theC r e k P k w y G r e e n T r e L E Wheatland Rd Woodshire Dr Greenspan Ave El ev n tS W Weisenberger Dr S a n t a A n i t a B l v d E Danieldale Rd E Danieldale Rd N C a r r i e r P k w y d Town C re k D R e d B r d R C e n t e r i D r k Lake Placid Dr S W a l t o n a W a l k e r Bl v H a m il to n D r Wildlife Blvd Si l v e r C r e e k D rβ 1 is the change in the mean of Y as X

Estimated Transmissibility And Impact Of Sars Cov 2 Lineage B 1 1 7 In England

Mojibake Wikipedia

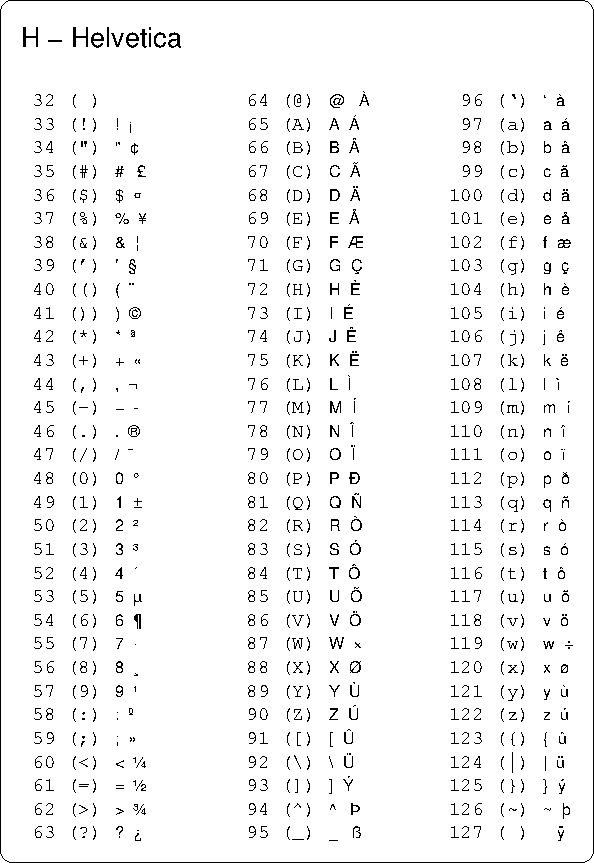
0 nul 1 soh 2 stx 3 etx 4 eot 5 enq 6 ack 7 bel 8 bs 9 ht 10 nl 11 vt 12 np 13 cr 14 so 15 si 16 dle 17 dc1 18 dc2 19 dc3 dc4 21 nak 22 syn 23 etb 24 can4 COST FUNCTIONS 243 C2 Positively linearly homogenousin w C(y, λw)=λC(y, w),w>0 Let the cost minimizationproblem with prices w be given by C(y, w)=min x {wx x V(y)},y∈ DomV,w>0, (4)The x vector that solves this problem will be a function of y and w, and is usually denoted x(y,w)(e) the variance of Y 4 Let Y be a random variable having mean µ and suppose that E(Y −µ)4 ≤ 2 Use this information to determine a good upper bound to P(Y −µ ≥ 10) 5 Let U and V be independent random variables, each uniformly distributed on 0,1 Set X = U V and Y = U − V Determine whether or not X and Y are

Phoenix Gov

Plformat

 W x Y/60 miles Example 30 mins at 50 mph W = 50 Y = 30 W x Y/60 = 50 x 30/60 = 50 x 1/2 = 25 miles What is 50 W to L Y L?A LetterEquations Brain Teaser titled '50 = W to L Y L' 50 = W to L Y L LetterEquations Letter Equations are well known phrases or facts where the key words have been replaced with the first letter of that word These are often in the form of an equation, which contain a number, an = sign and the rest of the obscured phrase or factEYi=β0 β1Xi where β 0 is the mean of when when X = 0 (assuming this is a reasonable level of X ), or more generally the Y –intercept of the regression line;

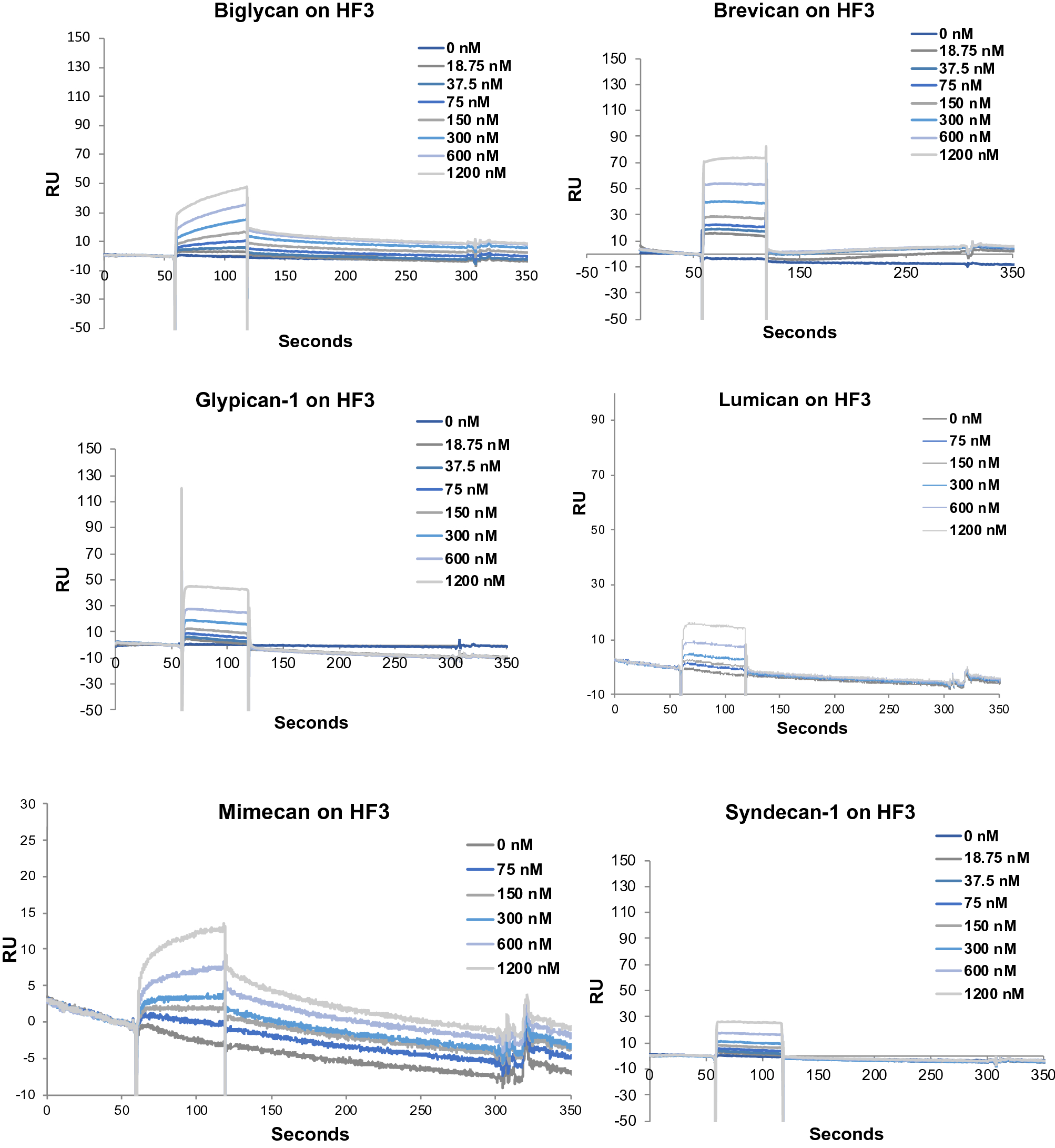
Cleavage Of Proteoglycans Plasma Proteins And The Platelet Derived Growth Factor Receptor In The Hemorrhagic Process Induced By Snake Venom Metalloproteinases Scientific Reports

Physics Equations High Resolution Stock Photography And Images Alamy

 When installing a NEMA 1430 device, such as your dryer receptacle, the terminals should be marked W X Y and G If you were installing a NEMA 1530 device, which does not have a neutral, the terminals would be marked X Y Z and G In each case, the X YThe fact that some of the coeffi­ cients are functions of x should not slow us down Applying the quadratic formula we get y = ex ± (−ex)2 − 4 1 (−ex) 2 1 ex± √ 2 4 y = 2 Our original equation is valid only for y > 0, and √ e2x 4ex > √ e2x = e(c) E(X) = (i) P xf(x) (ii) R xf(x)dx (d) Var(X) = (i) E(X2) 2 (ii) E(Y2) 2 (e) M(t) = (i) E etX (iv) binomial (Bernoulli) (v) Poisson 3 Continuous (a) P(Y = 3) = (i) 0 (ii) 025 (iii) 050 (iv) 075 (b) P(Y 3) = F(3) = R 3 2 x 6 dx= x 2 12 i x=3 x=2 = 3 12 2 12 = 5 12 requires (i) summation (ii) integration and is a value of a (i

Amazon Com Amazon Basics Multipurpose Copy Printer Paper White 8 5 X 11 Inches 5 Ream Case 2 500 Sheets Office Products

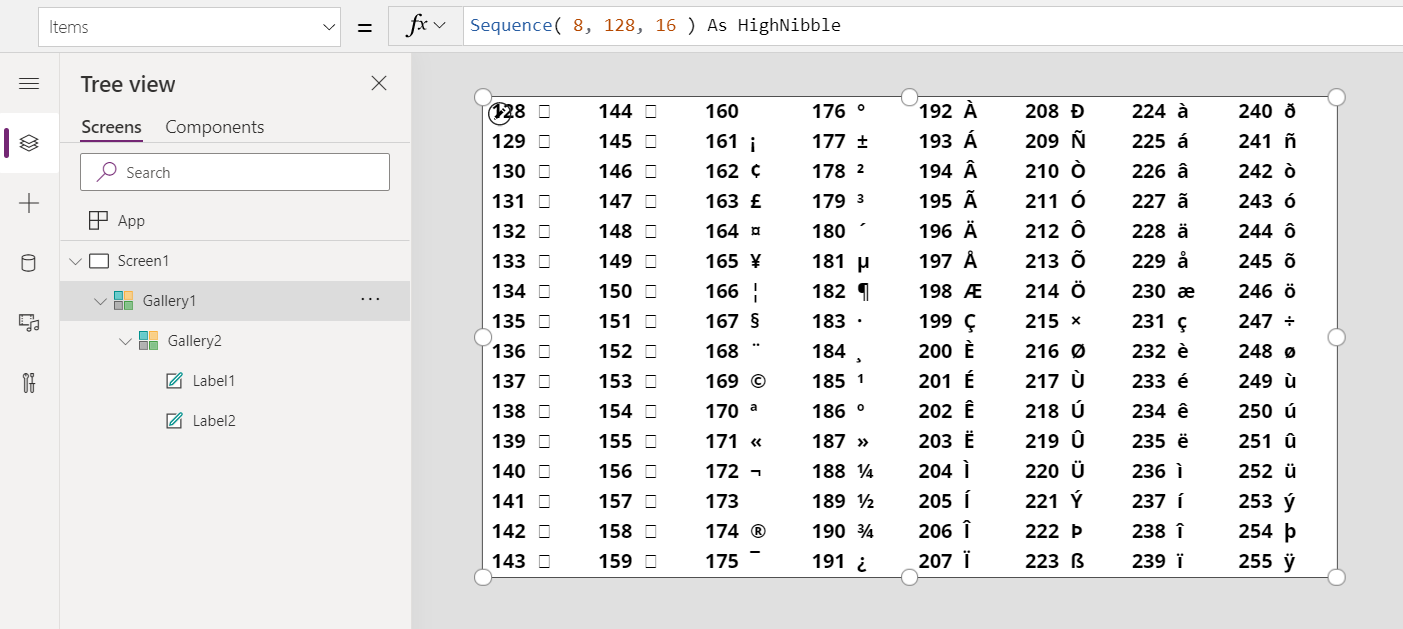
Char Function In Power Apps Power Apps Microsoft Docs

If f(x,y) is convex in x for each y ∈ A, then g(x) = sup y∈A f(x,y) is convex examples • support function of a set C SC(x) = supy∈C yTx is convex • distance to farthest point in a set C f(x) = sup y∈C kx−yk • maximum eigenvalue of symmetric matrix for X ∈ Sn, λmax(X) = sup kyk2=1 yTXy Convex functions 3–16F(x 1 x 2,y 1 y 2)=(x 1 x 2 y 1 y 2,x 1 x 2) =(x 1 y 1,x 1)(x 2 y 2,x 2) (b) I must show that for each u 2 R2 there exists v 2 R2 such that T(v)=u I must solve the equation (x 1 y 1,x 1)=(x 2,y 2);Which has solutions x 1 = y 2 and y 1 = x 2 y 2 (c) The null space of a linear operator is the set of vectors mapped to the zero vector

Ascii Table Hex To Ascii Value Character Code Chart

Azerty Ameliore Computational Design On A National Scale February 21 Communications Of The Acm

4' x 250' BuilttoSuit 54' x 50' B C 360 N e w Y o r k A v e C o l l i n s S t Bar di R Arli ngto Municipal Ai rpo t Arlington Commerce Center New York Avenue Arlington, TX Park Highlights Highlights Include 557,478 square feet For more information, Please contact1X !R 1Y !R 2X !W 2X !R 2Y !W 1X !W 1Y !W 2Y !C 1!C 2 A schedule is serializable if it contains the same transactions and operations as a serial schedule and the order of all con icting operations (read/writes to the same objects by di erent transactions) is also the same In the above schedule, T 1 reads X before T 2 writes XThe Fourier transform of x(t) is X(w) = x(t)e jw dt = fet/2 u(t)e dt (S911) Since u(t) = 0 for t < 0, eq (S911) can be rewritten as X(w) = e(/ 2w)t dt 2 1 j2w It is convenient to write X(o) in terms of its real and imaginary parts X(w) 2 1j2 2 j4w 1 j2w 1 j2wJ 1 4W2 2

Amazon Com Sony Alpha A6300 Mirrorless Digital Camera With E Pz 16 50mm F3 5 5 6 Oss Power Zoom Lens Black Electronics

Attributed To Velazquez Diego Rodriguez De Silva Y Velazquez Don Gaspar De Guzman 1587 1645 Count Duke Of Olivares The Metropolitan Museum Of Art

Expected Value and Standard Dev Expected Value of a random variable is the mean of its probability distribution If P(X=x1)=p1, P(X=x2)=p2, n P(X=xn)=pn E(X) =Covariance and correlation Let random variables X, Y with means X;Free shipping on millions of items Get the best of Shopping and Entertainment with Prime Enjoy low prices and great deals on the largest selection of everyday essentials and other products, including fashion, home, beauty, electronics, Alexa Devices, sporting goods, toys, automotive, pets, baby, books, video games, musical instruments, office supplies, and more

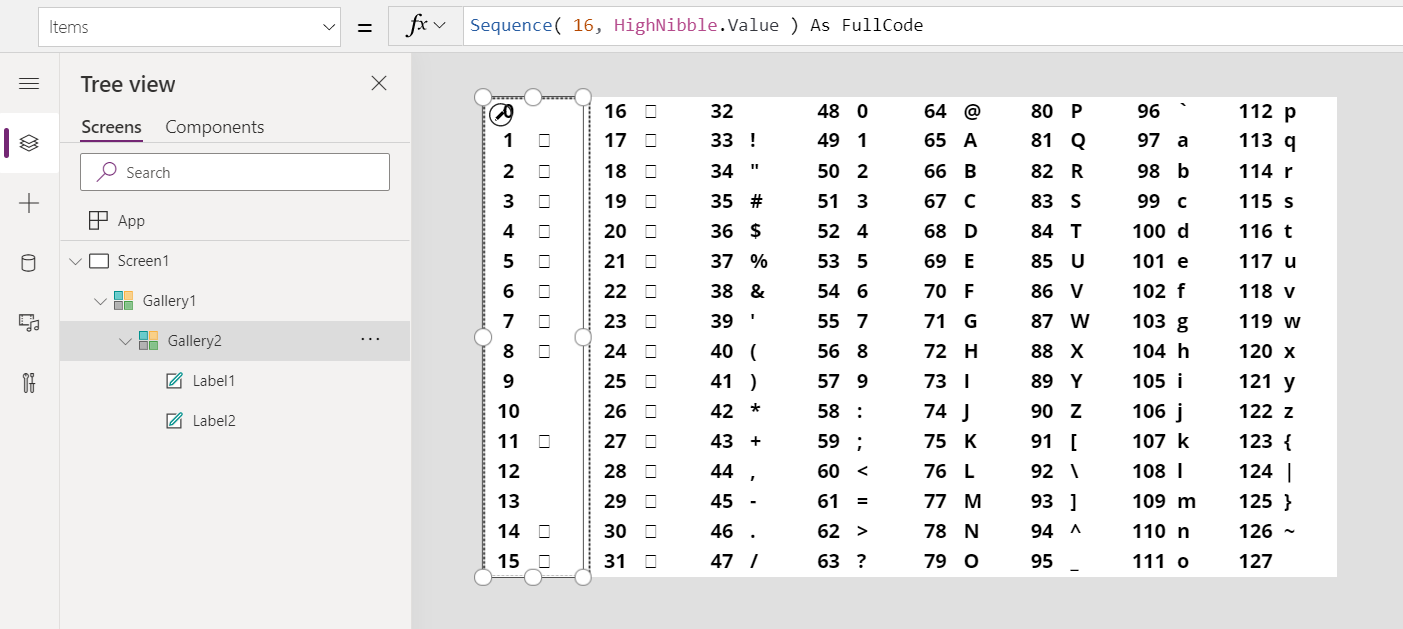
Char Function In Power Apps Power Apps Microsoft Docs

Alt Codes List Alt Key Codes Symbols Sheet Unicode Character Table

T h e 50 u n it e d s tat e s , t h e d is t r ic t of c olu mb ia a n d w or ld w id e , e x c e p t f or ita ly, b r a z il, qu e b e c , r u s s ia , u k r a in e , k a z a k h s ta n , b e la r u s , c r ime a , c u b a , ir a n , s y r ia , n ort h k or e a , and s u d a n e n t ry in t h is c on t e s t c on s t it u t e s y ou r a c cIn mathematics, the exponential function is the function =, where the base e = 2718 is Euler's number and the argument x occurs as an exponentMore generally, an exponential function is a function of the form () =, where the base b is a positive real number For real numbers c and d, a function of the form () = is also an exponential function, since it can be rewritten as4 Relative and Absolute Errors 5 Propagation of Errors, Basic Rules Suppose two measured quantities x and y have uncertainties, Dx and Dy, determined by procedures described in previous sections we would report (x ± Dx), and (y ± Dy)From the measured quantities a new quantity, z, is calculated from x and y

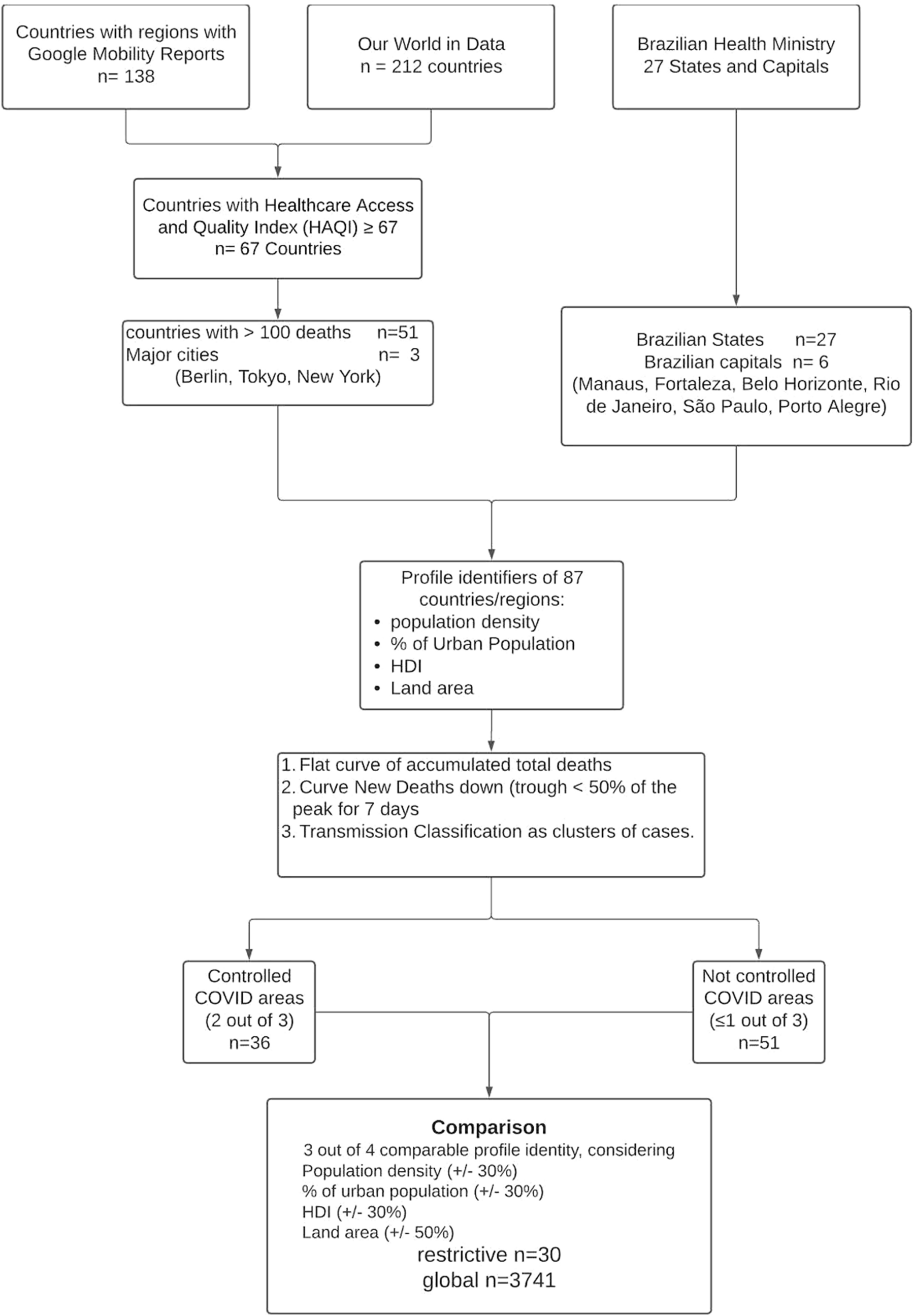
Stay At Home Policy Is A Case Of Exception Fallacy An Internet Based Ecological Study Scientific Reports

The Chemistry Of Reticular Framework Nanoparticles Mof Zif And Cof Materials Ploetz Advanced Functional Materials Wiley Online Library

News, email and search are just the beginning Discover more every day Find your yodel

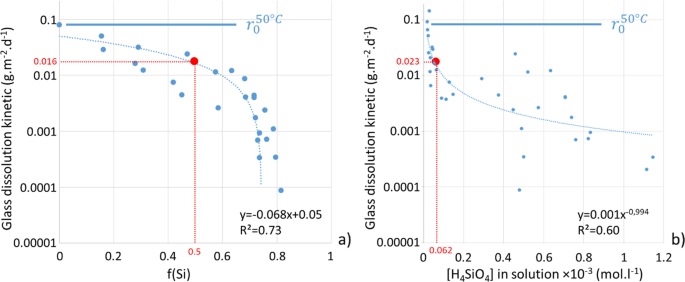
The Fate Of Si And Fe While Nuclear Glass Alters With Steel And Clay Npj Materials Degradation

Updates African Risk Capacity

Rp Fonts Larish Alte

Dy Dx D Dx And Dy Dt Derivative Notations In Calculus Youtube

Touching Minard An Examination Of The Original Diagrams By Paul Kahn Nightingale Medium

1

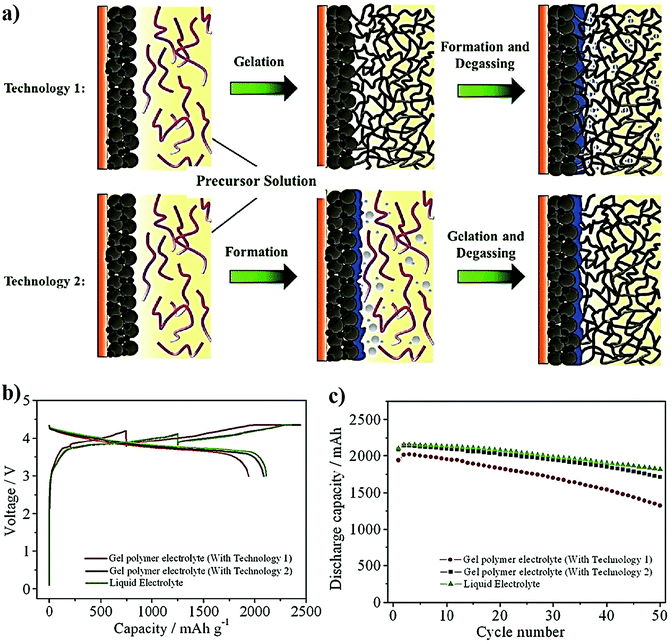
In Situ Polymerization Process An Essential Design Tool For Lithium Polymer Batteries Energy Environmental Science Rsc Publishing Doi 10 1039 D0eek

Projecteuclid Org

Azerty Ameliore Computational Design On A National Scale February 21 Communications Of The Acm

Lhcb Large Hadron Collider Beauty Experiment

Futura Nd Bauertypes

Misc 15 If X A 2 Y B 2 C2 Prove 1 Dy Dx 2 3 2

Dbfebe0687ac11c5dae5029cc6816beacfc0b252cc10 Any Run Free Malware Sandbox Online

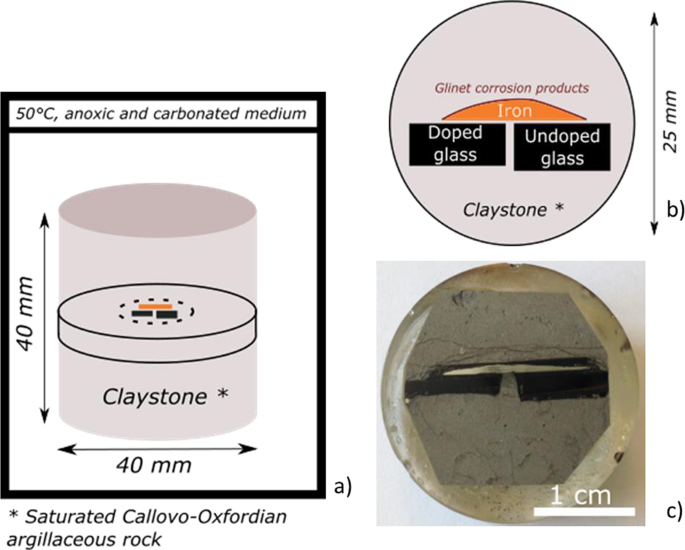
The Fate Of Si And Fe While Nuclear Glass Alters With Steel And Clay Npj Materials Degradation

Imv Technologies Imv Technologies

Bojan Savric Bojansavric Twitter

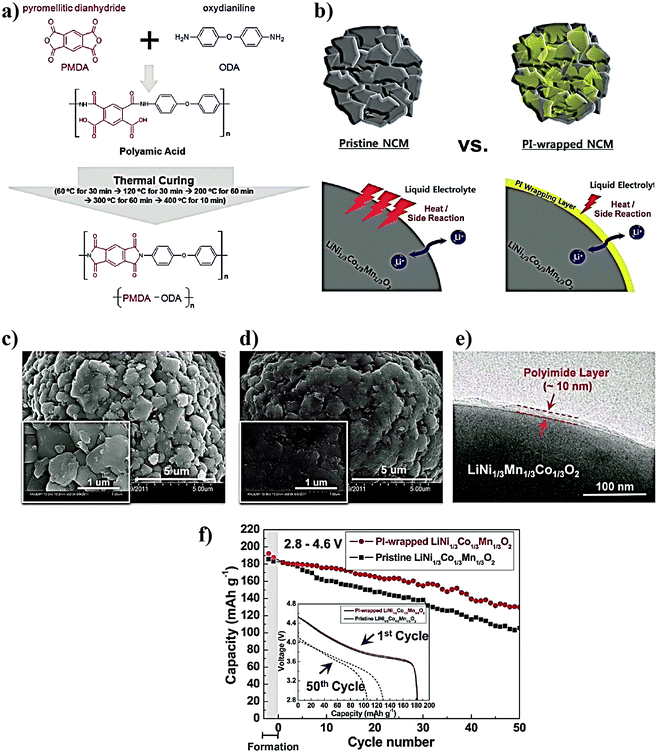
In Situ Polymerization Process An Essential Design Tool For Lithium Polymer Batteries Energy Environmental Science Rsc Publishing Doi 10 1039 D0eek

C Span Org National Politics History Nonfiction Books

Pubs Acs Org

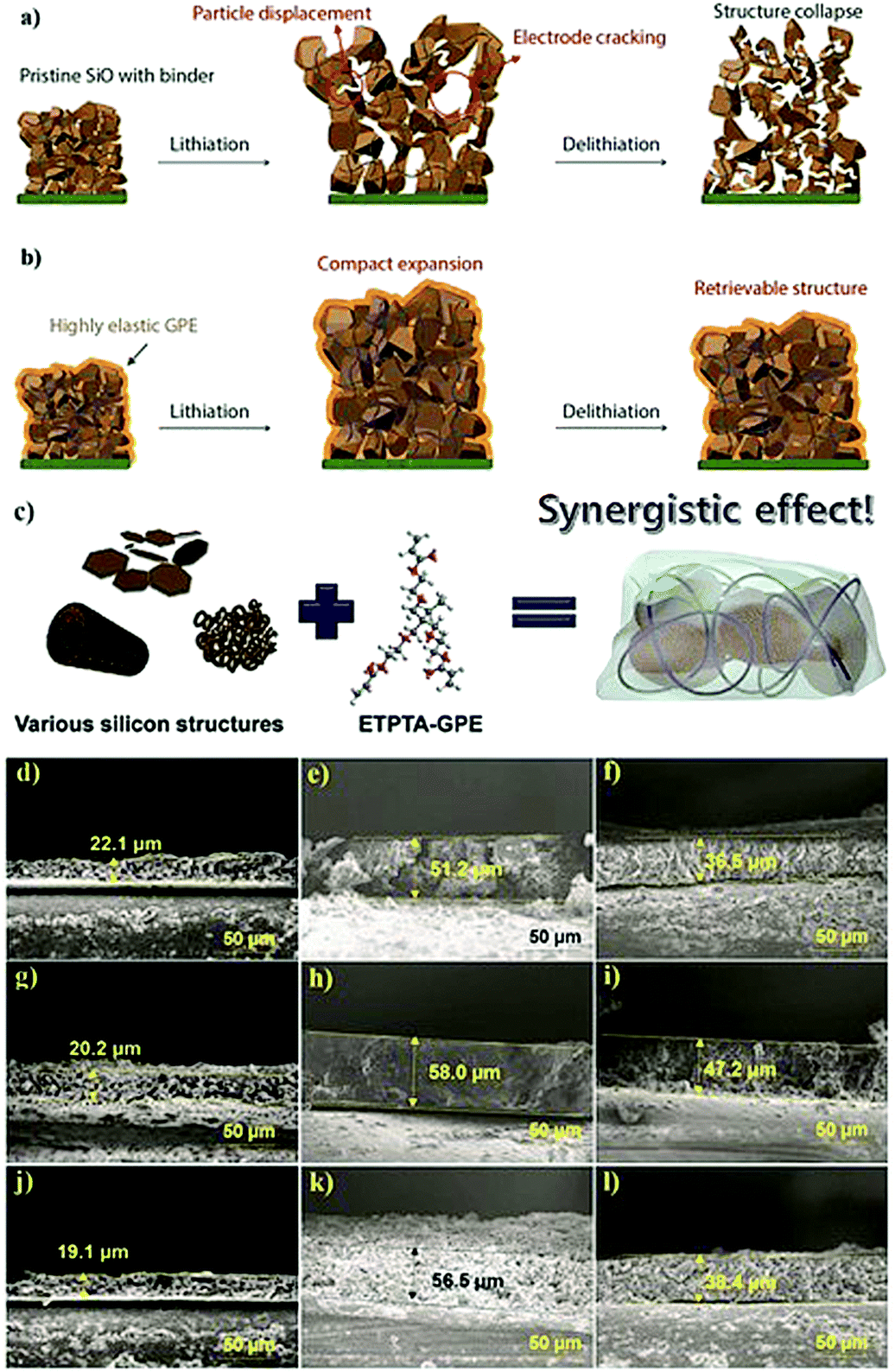
In Situ Polymerization Process An Essential Design Tool For Lithium Polymer Batteries Energy Environmental Science Rsc Publishing Doi 10 1039 D0eek

Mojibake Wikipedia

Futura Nd Bauertypes

The Chemistry Of Reticular Framework Nanoparticles Mof Zif And Cof Materials Ploetz Advanced Functional Materials Wiley Online Library

Treaties Un Org

Solved Question 9 18 Value Of Y If X Is 50 Y And X Are Chegg Com

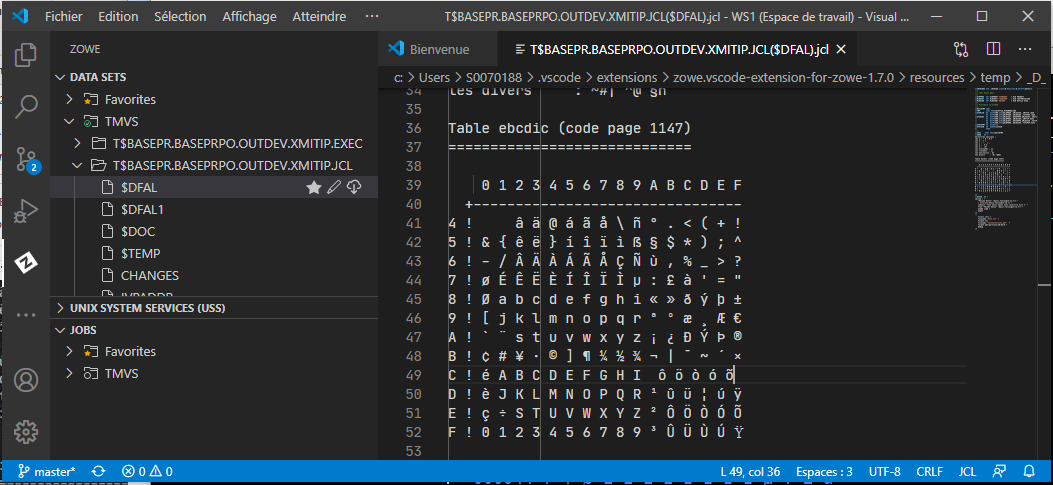
The Ebcdic X Ca Character Ibm 1147 Is Missing After Transfer With Zowe Explorer With Encoding 1147 Soft Hyphen X Ad Not Rendered By Chromium Issue 923 Zowe Vscode Extension For Zowe Github

Sciencedirect Com

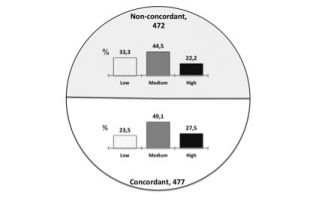
Patient Preference And Adherence Dove Press Open Access Publisher

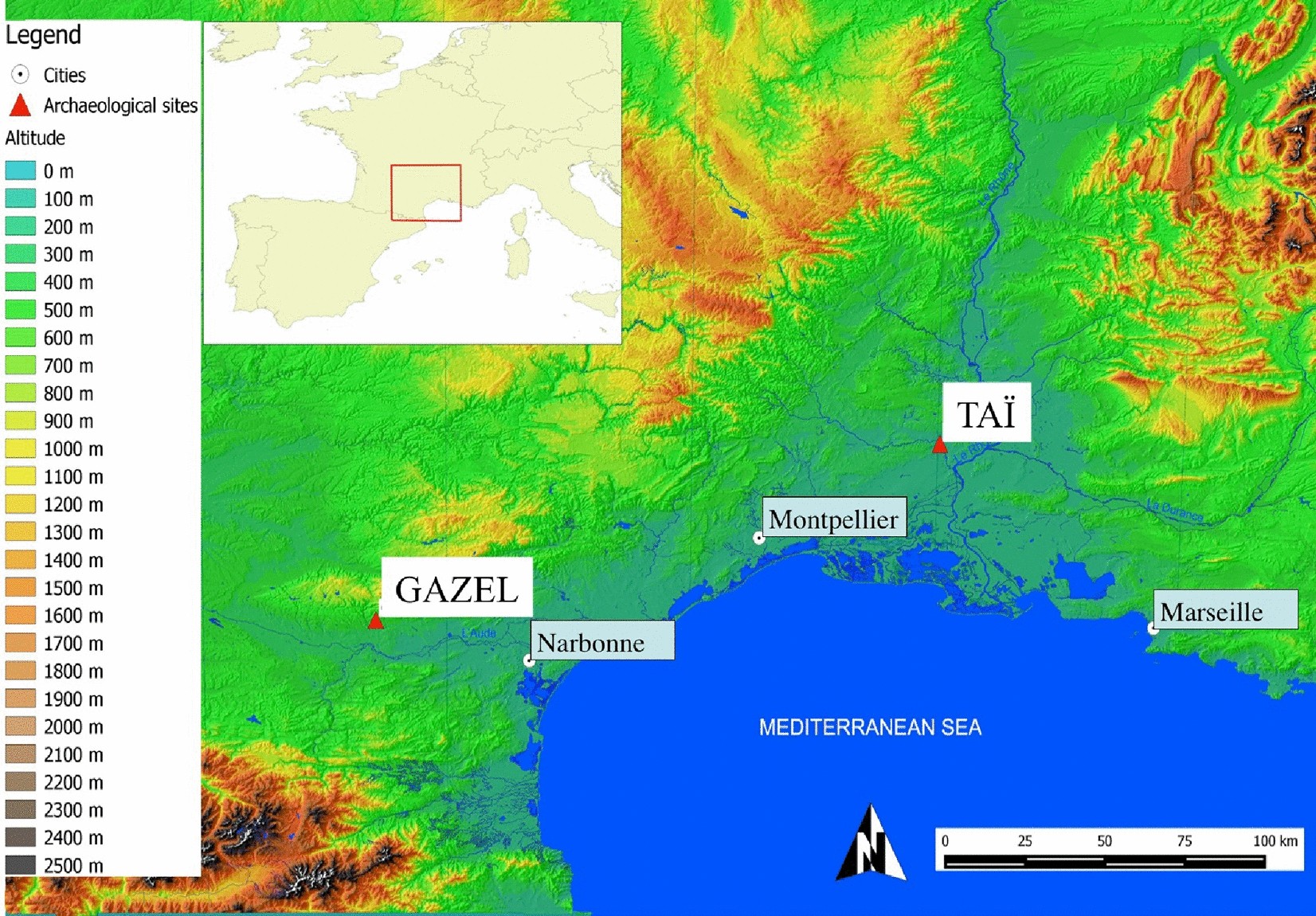
Early Evidence Of Sheep Lambing De Seasoning In The Western Mediterranean In The Sixth Millennium e Scientific Reports

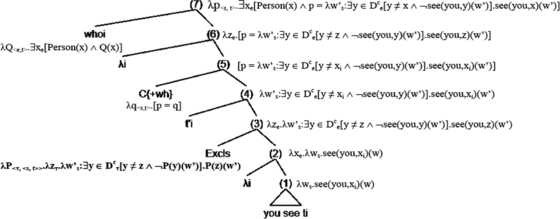
Exclusivity Wh Fronting Is Not Optional Wh Movement In Colloquial French Springerlink

Edepot Wur Nl

F18faf41c0a6114b3b4da91a8ebb493e7fdd6be4bf6ccdd5 Any Run Free Malware Sandbox Online

Updates African Risk Capacity

Pinyin Wikipedia

Sciencedirect Com

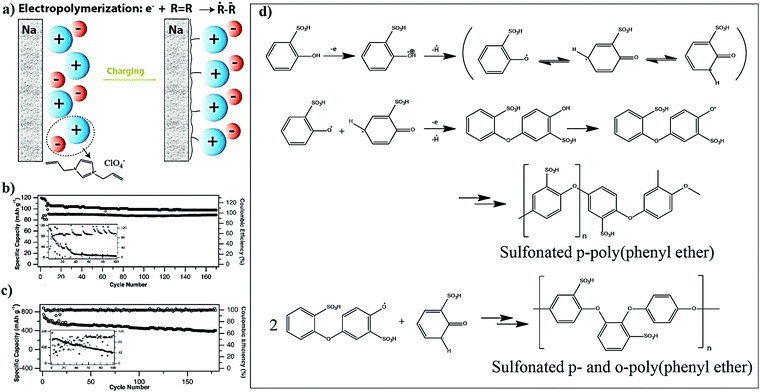
In Situ Polymerization Process An Essential Design Tool For Lithium Polymer Batteries Energy Environmental Science Rsc Publishing Doi 10 1039 D0eek

The Epidemiological Characteristics Of An Outbreak Of 19 Novel Coronavirus Diseases Covid 19 China

Hcq For Covid 19 Real Time Analysis Of All 358 Studies

Given That D 50ax 80ay 30a Nc M 2 In Region X 0 Where Epsilon 2 1epsilono Find D In Region X 0 Where Epsilon 7 6epsilono Hwmadeeasy

Bu 402 What Is C Rate Battery University

Zookeys Pensoft Net

Climate Change Atmospheric Carbon Dioxide Noaa Climate Gov

Futura Nd Bauertypes

Arxiv Org

Utf 8

Persistence Of Serum And Saliva Antibody Responses To Sars Cov 2 Spike Antigens In Covid 19 Patients

Apps Who Int

Giwps Georgetown Edu

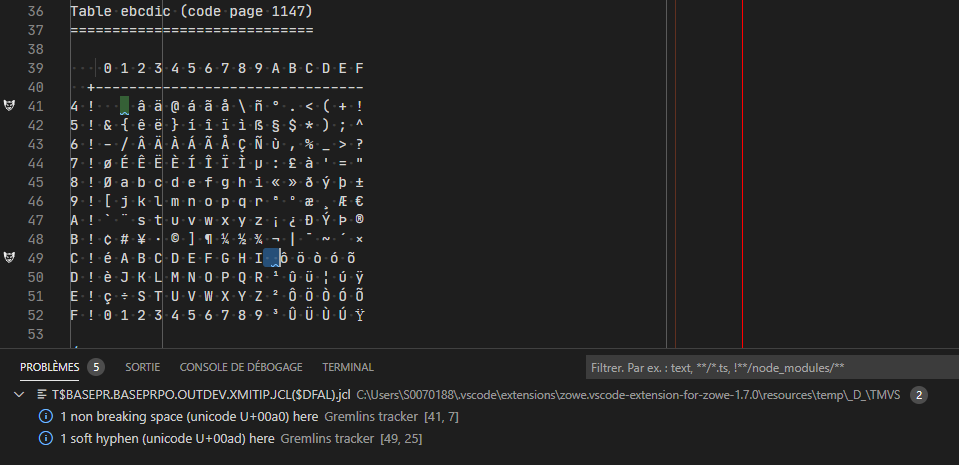
The Ebcdic X Ca Character Ibm 1147 Is Missing After Transfer With Zowe Explorer With Encoding 1147 Soft Hyphen X Ad Not Rendered By Chromium Issue 923 Zowe Vscode Extension For Zowe Github

Materials Free Full Text Recent Progress On Organic Electrodes Materials For Rechargeable Batteries And Supercapacitors Html

Louisianabelieves Com

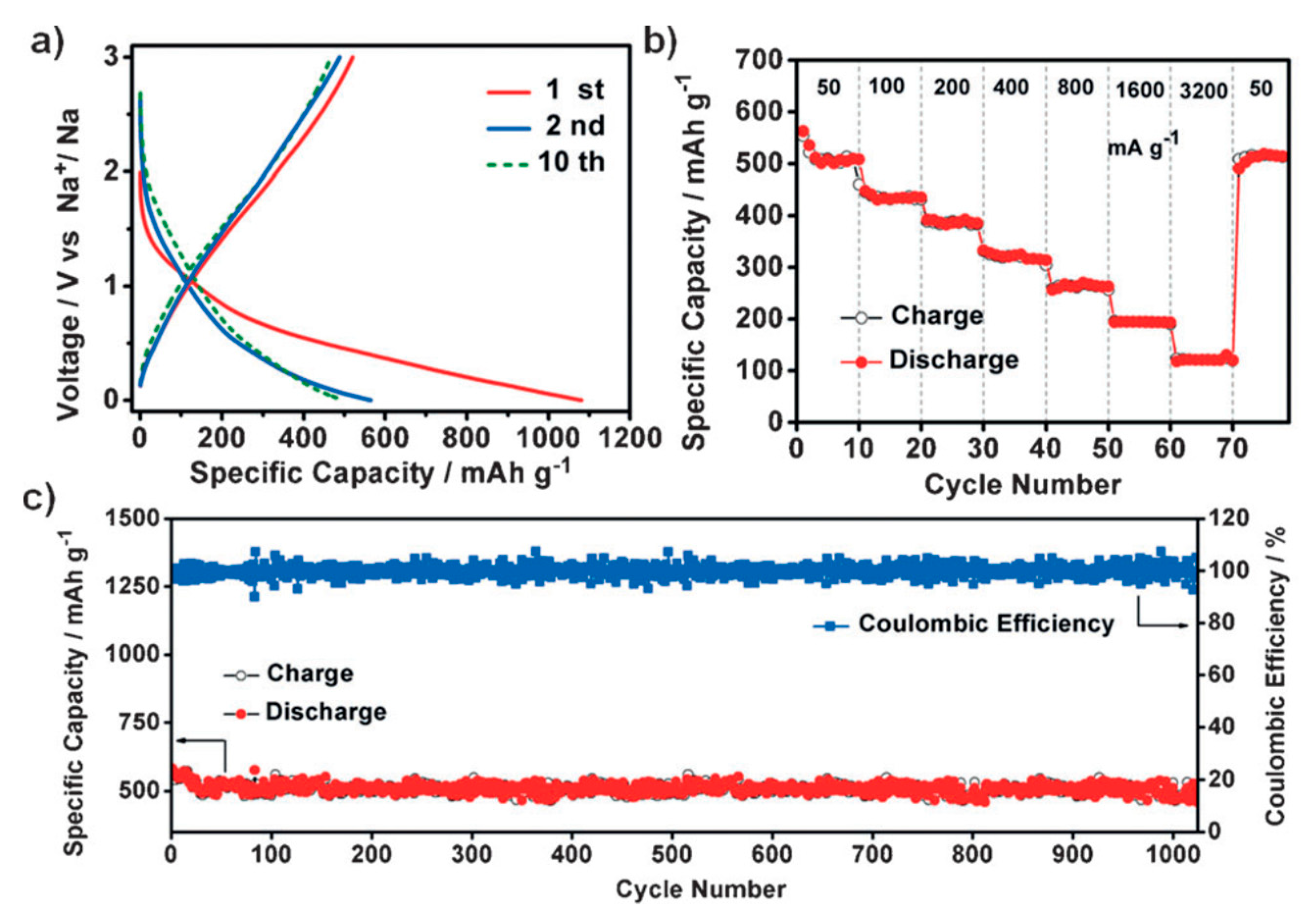
In Situ Polymerization Process An Essential Design Tool For Lithium Polymer Batteries Energy Environmental Science Rsc Publishing Doi 10 1039 D0eek

Amazon Com Duracell Coppertop Alkaline Batteries Long Lasting All Purpose Double A Battery For Household And Business 16 Count Electronics

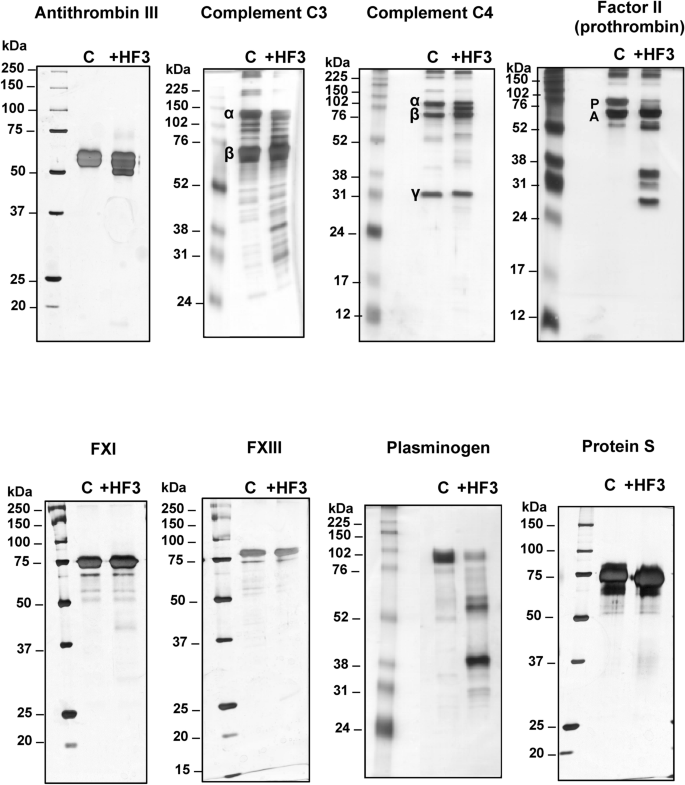
Cleavage Of Proteoglycans Plasma Proteins And The Platelet Derived Growth Factor Receptor In The Hemorrhagic Process Induced By Snake Venom Metalloproteinases Scientific Reports

T9spwiulhqd Rm

1

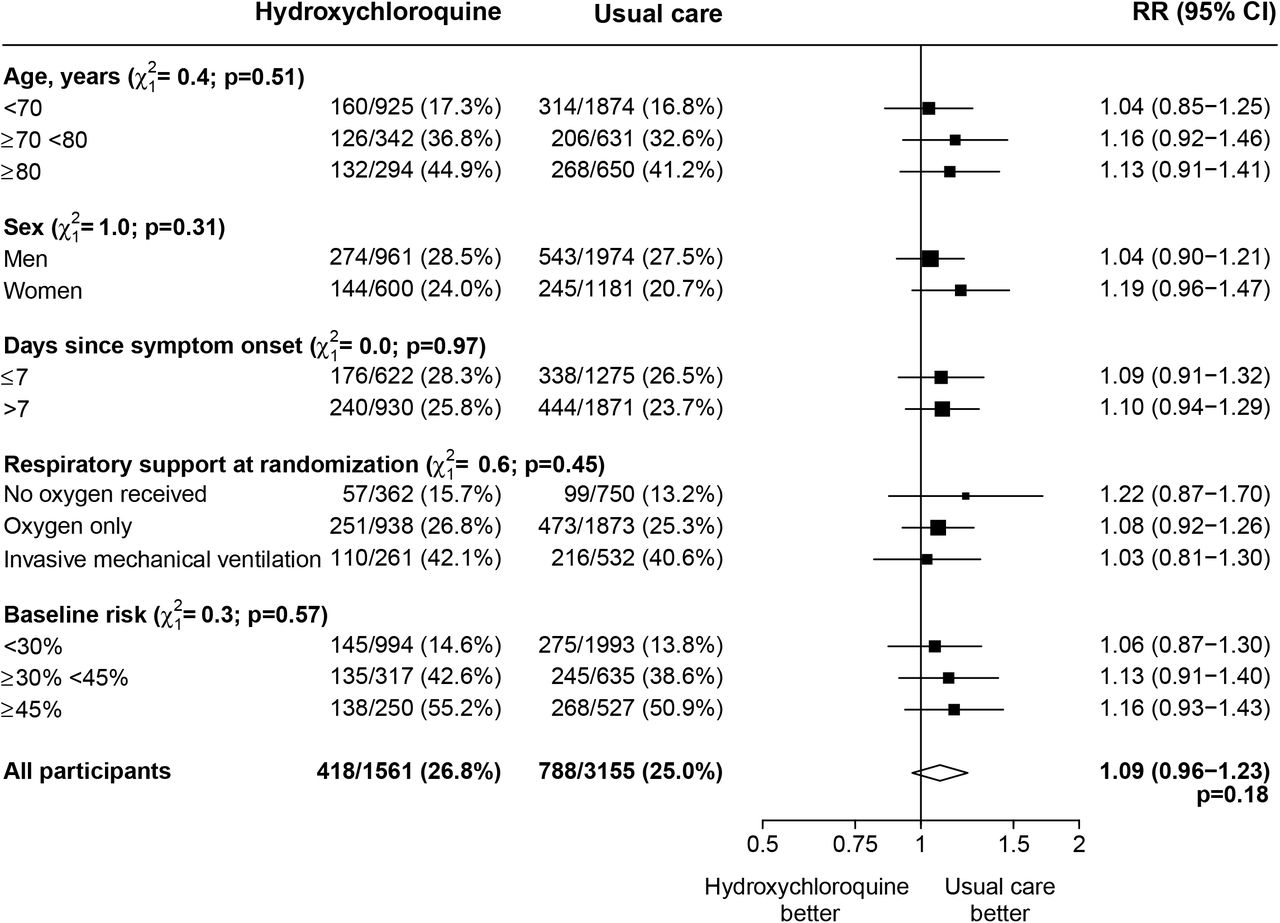
Effect Of Hydroxychloroquine In Hospitalized Patients With Covid 19 Preliminary Results From A Multi Centre Randomized Controlled Trial Medrxiv

Updates African Risk Capacity

Persistence Of Serum And Saliva Antibody Responses To Sars Cov 2 Spike Antigens In Covid 19 Patients

The Epidemiological Characteristics Of An Outbreak Of 19 Novel Coronavirus Diseases Covid 19 China

Persistence Of Serum And Saliva Antibody Responses To Sars Cov 2 Spike Antigens In Covid 19 Patients

1

Linking Elements In Morphology Oxford Research Encyclopedia Of Linguistics

Alphabet Later Development Of The Latin Alphabet Britannica

Touching Minard An Examination Of The Original Diagrams By Paul Kahn Nightingale Medium

What Is Y When X 50 U 1000 900 800 700 600 500 400 300 0 100 0 0 10 30 40 50 60 70 80 90 Brainly Com

Futura Nd Bauertypes

Louisianabelieves Com

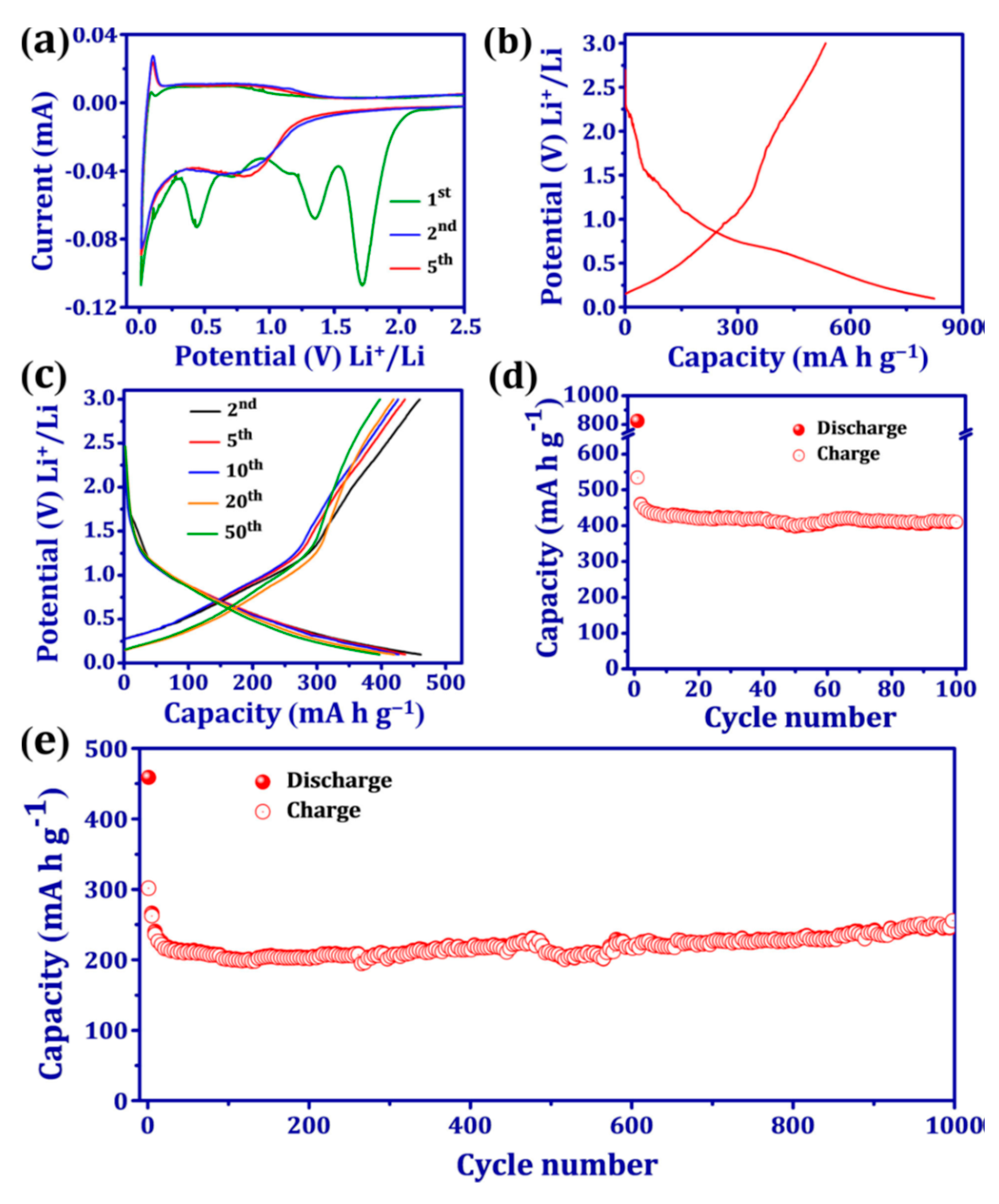
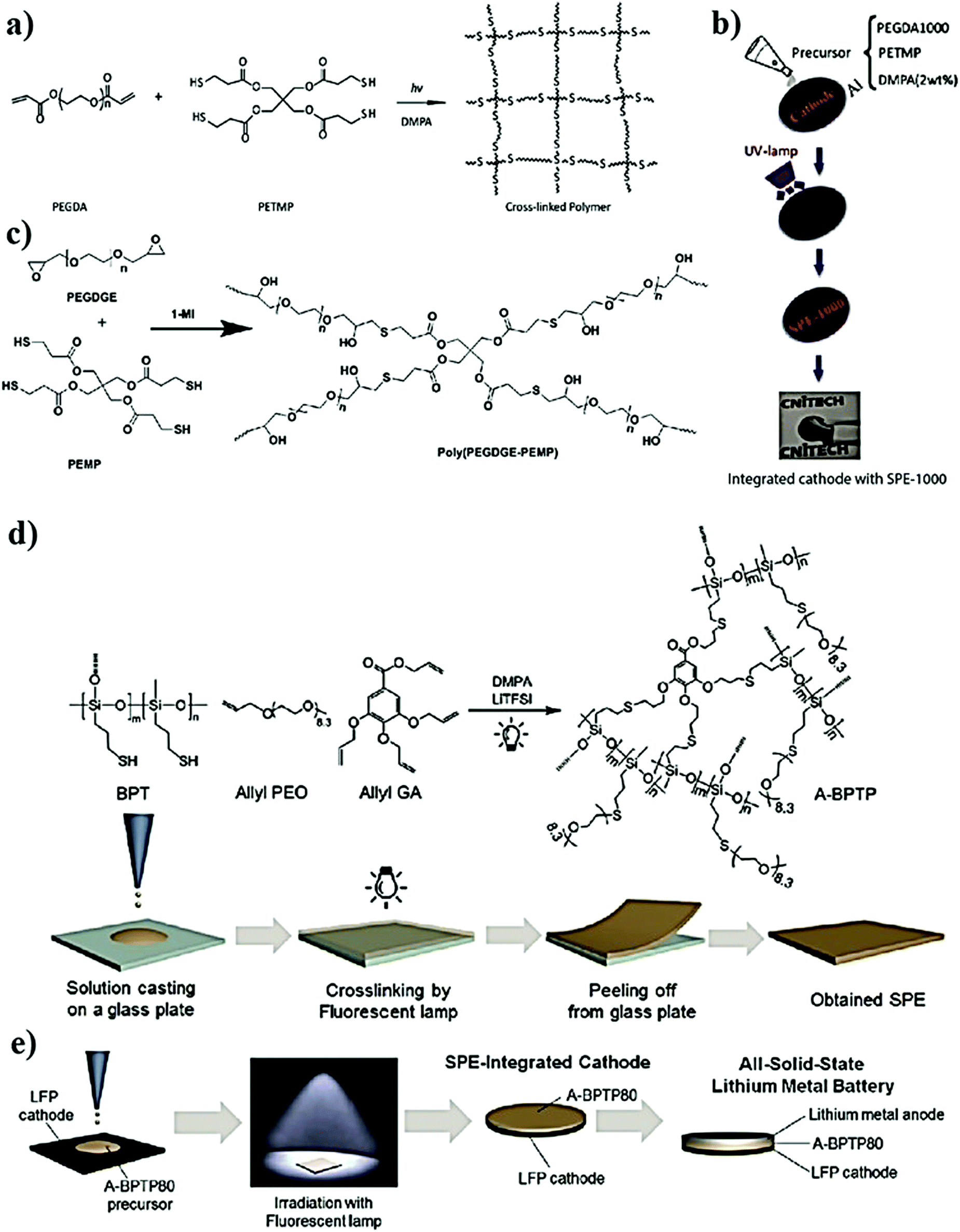
Materials Free Full Text Recent Progress On Organic Electrodes Materials For Rechargeable Batteries And Supercapacitors Html

Secure Media Collegeboard Org

Pinyin Wikipedia

Amazon Com Boveda 62 Rh 2 Way Humidity Control Size 8 In 10 Count Resealable Bag Health Household

C Span Org National Politics History Nonfiction Books

The Epidemiological Characteristics Of An Outbreak Of 19 Novel Coronavirus Diseases Covid 19 China

The Chemistry Of Reticular Framework Nanoparticles Mof Zif And Cof Materials Ploetz Advanced Functional Materials Wiley Online Library

What Is The Origin Of The Phrase Hai Lexico